6 Implausibility

A video presentation of this section can be found here.

We will first briefly review the definition of an implausibility measure.

For a given stochastic model output and a given target, the implausibility measures the difference between the output and the target, taking into account all sources of uncertainty. For a parameter set \(x\), a particular choice of implausibility, useful for either matching to the mean of the stochastic model, or its spread of possible values, is:

\[\text{Imp}(x) = \frac{|\text{E}[m(x)]-z|}{\sqrt{V_0 + V_c(x)+V_s(x)+V_m}},\]

where \(\text{E}[m(x)]\) is the expected value of the mean of the stochastic model, \(z\) the target, and the terms in the denominator refer to various forms of uncertainty. In particular

• \(V_0\) is the variance associated with the observation uncertainty;
• \(V_c(x)\) refers to the uncertainty one introduces when using the emulator output instead of the model output itself;
• \(V_s(x)\) is the ensemble variability and represents the stochastic nature of the model. This term is used to create an appropriate representation of the uncertainty on either the mean or the set of possible realisations of the stochastic model.
• \(V_m\) is the model discrepancy, accounting for possible mismatches between the model and reality.

Since in this case study we want to emulate our model, without reference to a real-life analogue, the model represents the reality perfectly. For this reason we have \(V_m=0\). The term \(V_s\), which was zero when we worked on the deterministic SEIRS model (Workshop 1), is now non-zero, in order to account for the stochasticity of the model.

A very large value of \(\text{Imp}(x)\) means that we can be confident that the parameter set \(x\) does not provide a good match to the observed data, even factoring in the additional uncertainty that comes with the use of emulators.

To plot the maximum implausibility (across all emulators), we set plot_type to nimp in the call to emulator_plot:

emulator_plot(stoch_emulators, plot_type = 'nimp', 
              targets = targets, params = c('epsilon', 'alpha'))

Task

Use the argument fixed_vals to set the parameters that are not shown in the plot to be as in chosen_params. Verify that the implausibility at chosen_params is below 3.

Solution

We set fixed_vals to chosen_params[!names(chosen_params) %in% c('epsilon', 'alpha')], plot the maximum implausibility and add a point corresponding to the values of \(\sigma\) and \(alpha\) in chosen_params:

emulator_plot(stoch_emulators, plot_type = 'nimp', targets = targets,
              params = c('epsilon', 'alpha'),
              fixed_vals = chosen_params[!names(chosen_params) %in% c('epsilon', 'alpha')], 
              cb=T) +geom_point(aes(x=1/7, y=1/50), size=3)

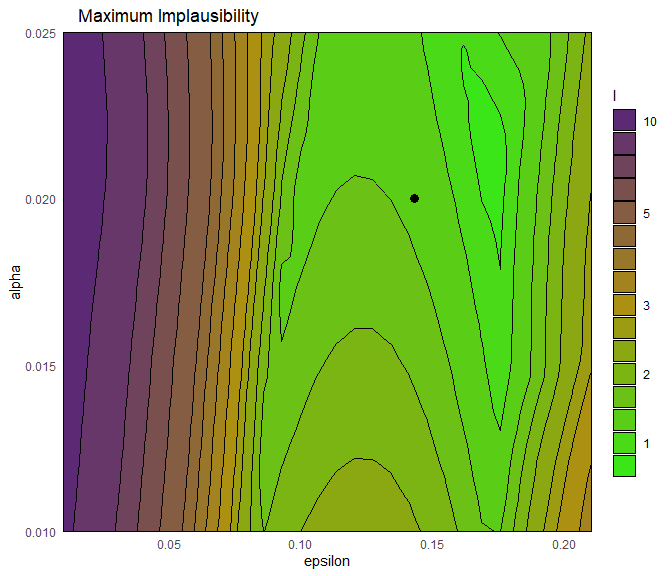The plot shows what we expected: when \(\epsilon\) and \(\alpha\) are equal to their values in chosen_params, the implausibility measure is below the threshold \(3\) (cf. black point in the box).