8 Proposing new points

In this section we generate the set of points that will be used to train the second wave of emulators. Through visualisations offered by hmer, we then explore these points and assess how much of the initial input space has been removed by the first wave of emulators.

The function generate_new_design is designed to generate new sets of parameters; its default behaviour is as follows.

STEP 1. A set of parameter sets is generated using a Latin Hypercube Design, rejecting implausible parameter sets.

STEP 2. Pairs of parameter sets are selected at random and more sets are sampled from lines connecting them, with particular importance given to those that are close to the non-implausible boundary.

STEP 3. Using these as seeding points, more parameter sets are generated using importance sampling to attempt to fully cover the non-implausible region.

Let us generate \(180\) new sets of parameters, using the emulators for the time up to \(t=200\). Focusing on early time outputs can be useful when performing the first waves of history matching, since the behaviour of the epidemic at later times will depend on the behaviour at earlier times. Note that the generation of new points might require a few minutes.

restricted_ems <- ems_wave1[c(1,2,3,4,7,8,9,10)]
new_points_restricted <- generate_new_design(restricted_ems, 180, targets, verbose=TRUE)

## Proposing from LHS...
## LHS has high yield; no other methods required.
## Selecting final points using maximin criterion...

We now plot new_points_restricted through plot_wrap. Note that we pass ranges to plot_wrap as well, to ensure that the plot shows the entire range for each parameter: this allows us to see how the new set of parameters compares with respect to the original input space.

plot_wrap(new_points_restricted, ranges)

By looking at the plot we can learn a lot about the non-implausible space. For example, it seems clear that low values of \(\gamma\) cannot produce a match (cf. penultimate column). We can also deduce relationships between parameters: \(\beta_1\) and \(\epsilon\) are an example of negatively-correlated parameters. If \(\beta_1\) is large then \(\epsilon\) needs to be small, and vice versa.

Now that we have generated a new set of points, we can compare the model output at points in initial_points with the model output at points in new_points_restricted

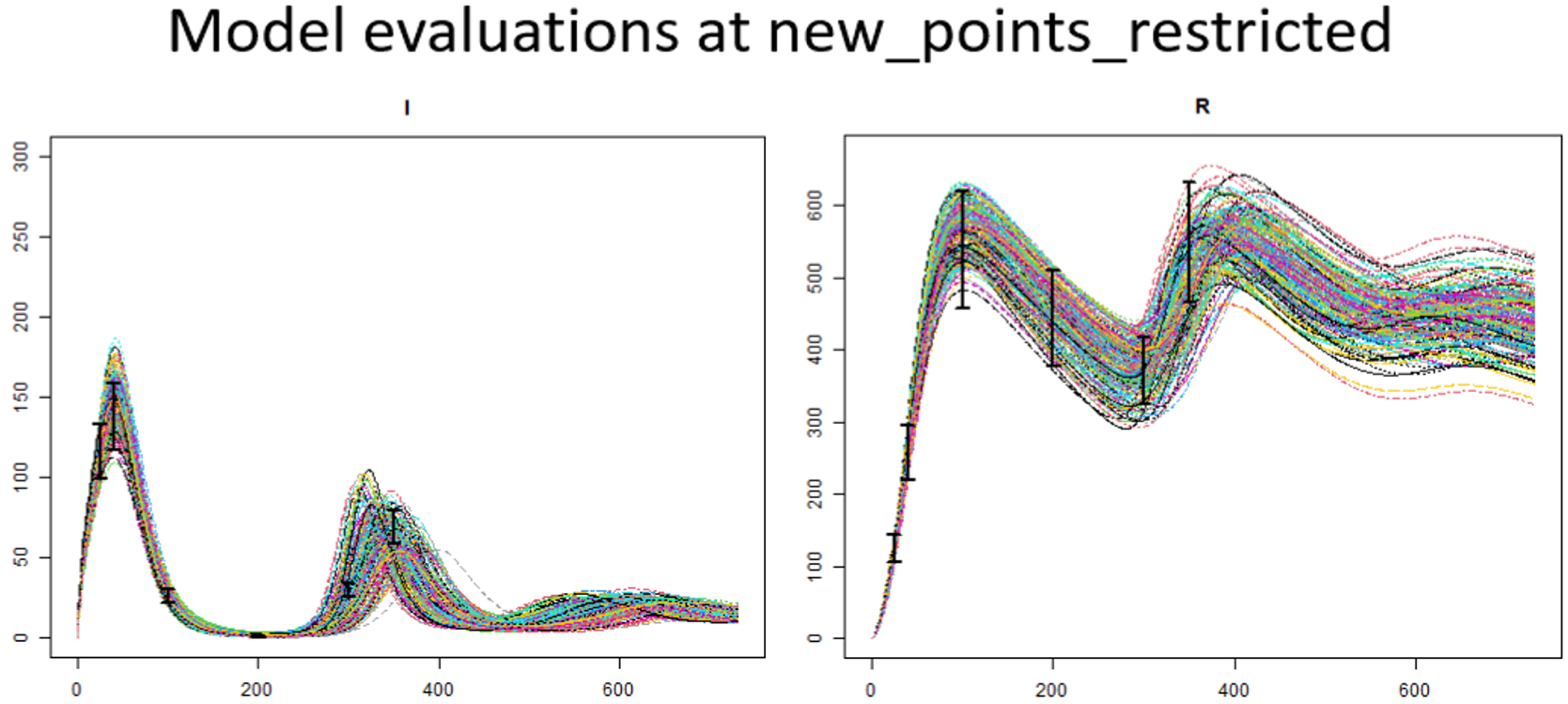
We can clearly see that the range of possible results obtained when evaluating the model at wave0 points is larger than the range obtained when evaluating the model at points in new_points_restricted. This is because we have performed a wave of the history matching process, discarding part of the initial input space that is not compatible with the targets.

Task

What do you think would happen if we tried generating new parameter sets using all emulators, instead of those relating to times up to \(t=200\) only? Try changing the code and seeing what happens.

Solution

We expect that using all emulators (instead of just a subset of them) will make the non-implausible space smaller than before, since more conditions will have to be met. Let us check if our intuition corresponds to what the plots show:

new_points <- generate_new_design(ems_wave1, 180, targets, verbose = TRUE)

## Proposing from LHS...
## LHS has high yield; no other methods required.
## Selecting final points using maximin criterion...

plot_wrap(new_points, ranges)

The answer is yes: points now look slightly less spread than before, i.e. a higher part of the input space has been cut-out.

In order to quantify how much of the input space is removed by a given set of emulators, we can use the function space_removed, which takes a list of emulators and a list of targets we want to match to. The output is a plot that shows the percentage of space that is removed by the emulators as a function of the implausibility cut-off. Note that here we also set the argument ppd, which determines the number of points per input dimension to sample at. In this workshop we have \(9\) parameters, so a ppd of \(3\) means that space_removed will test the emulators on \(3^9\) sets of parameters.

space_removed(ems_wave1, targets, ppd=3) + geom_vline(xintercept = 3, lty = 2) + 
  geom_text(aes(x=3, label="x = 3",y=0.33), colour="black", 
  angle=90, vjust = 1.2, text=element_text(size=11))

## Warning in geom_text(aes(x = 3, label = "x = 3", y = 0.33), colour = "black", :
## Ignoring unknown parameters: `text`

By default the plot shows the percentage of space that is deemed implausible both when the observational errors are exactly the ones in targets and when the observational errors are \(80\%\) (resp. \(90\%\), \(110\%\) and \(120\%\)) of the values in targets. Here we see that with an implausibility cut-off of \(3\), the percentage of space removed is around \(98\%\), when the observational errors are \(100\%\) of the values in targets. With the same implausibility cut-off of \(3\), the percentage of space removed goes down to \(97\%\), when the observational errors are \(120\%\) of the values in targets and it goes up to \(99\%\) when the observational errors are \(80\%\) of the values in targets. If instead we use an implausibility cut-off of \(5\), we would discard around \(88\%\) (resp. \(84\%\)) of the space when the observational errors are \(100\%\) of the values in targets (resp. when the observational errors are \(120\%\) of the values in targets). As expected, larger observational errors and larger implausibility cut-offs correspond to lower percentages of space removed.